В настоящее время наиболее распространены устройства отображения, кото­рые синтезируют изображения на плоскости - экране дисплея или бумаге. Устройства, которые создают истинно объемные изображения, пока доста­точно редки. Но все чаще появляются сведения о таких разработках, напри­мер, об объемных дисплеях или даже о трехмерных принтерах .

При использовании любых графических устройств обычно используют про­екции. Проекция задает способ отображения объектов на графическом уст­ройстве. Мы будем рассматривать только проекции на плоскость.

Мировые и экранные координаты

При отображении пространственных объектов на экране или на листе бумаги с помощью принтера необходимо знать координаты объектов. Мы рассмот­рим две системы координат. Первая - мировые координаты, которые опи­сывают истинное положение объектов в пространстве с заданной точностью. Другая - система координат устройства изображения, в котором осуществ­ляется вывод изображения объектов в заданной проекции.

Пусть мировые координаты будут трехмерными декартовыми координатами. Где должен размещаться центр координат, и какими будут единицы измерения вдоль каждой оси, пока для нас не очень важно. Важно то, что для изображения мы будем знать какие-то числовые значения координат отображаемых объектов.

Для получения изображения в определенной проекции необходимо рассчитать координаты проекции. Из них можно получить координаты для графического устройства- назовем их экранными координатами. Для синтеза изображения на плоскости достаточно двумерной системы координат. Одна­ко в некоторых алгоритмах визуализации используются трехмерные экранные координаты, например, в алгоритме Z-буфера.

Основные типы проекций

В компьютерной графике наиболее распространены параллельная и цент­ральная проекции (рис. 2.15).

Для центральной проекции (также называемой перспективной) лучи проеци­рования исходят из одной точки, размещенной на конечном расстоянии от объектов и плоскости проецирования. Для параллельной проекции лучи про­ецирования параллельны.

Аксонометрическая проекция

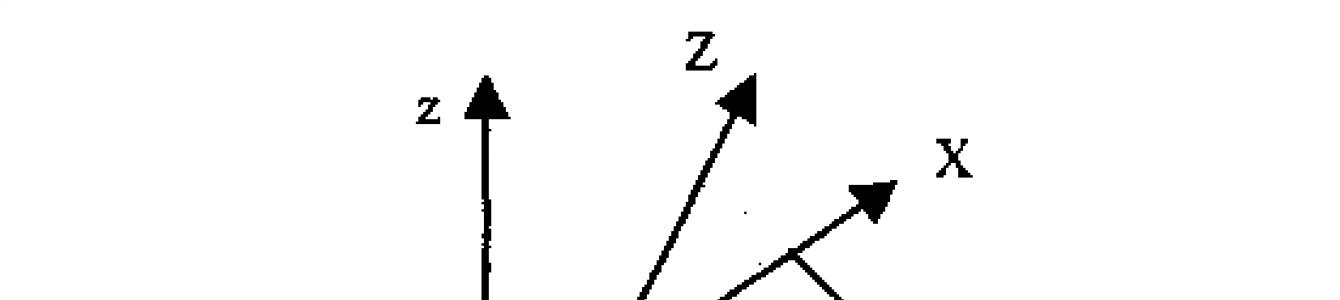
Аксонометрическая проекция - разновидность параллельной проекции. Для нее все лучи проецирования располагаются под прямым углом к плоскости проецирования (рис. 2.16).

[Зададим положения плоскости проецирования с помощью двух углов - α и β, Расположим камеру так, чтобы проекция оси z на плоскости проецирова|ния Х0Y была бы вертикальной линией (параллельной оси ОУ).

Рис. 2.16. Аксонометрическая проекция

Для того чтобы найти соотношения между координатами (х, у, z ) и (X , Y , Z ) для любой точки в трехмерном пространстве, рассмотрим преобразования системы координат (х , у, z ) в систему (X , Y , Z). Зададим такое преобразование двумя шагами.

1-й шаг. Поворот системы координат относительно оси z на угол α. Такой поворот осей описывается матрицей

2-й шаг. Поворачиваем систему координат (x ′, у", z ") относительно оси х" на угол β - получаем координаты (X , Y , Z ). Матрица поворота

Преобразования координат выражаем произведением матриц В * А:

Запишем
преобразование для координат проекции в виде формул:

Как вы считаете, будет ли получена та же проекция, если описывать преобра­зования координат теми же двумя шагами, но в другой последовательности - сначала поворот системы координат относительно оси х на угол β, а потом поворот системы координат относительно оси z " на угол α? И будут ли вер­тикальные линии в системе координат (x , y , z ) рисоваться также вертикалями в системе координат (X , У, Z)? Иначе говоря, выполняется ли А*В - В*А? Обратное преобразование координат аксонометрической проекции. Для того, чтобы координаты проекции (X , Y , Z ) преобразовать в мировые коорди­наты (х, у, z ), нужно проделать обратную последовательность поворотов. Вначале выполнить поворот на угол -β а затем - поворот на угол - α. Запи­шем обратное преобразование в матричном виде

Матрицы поворотов:

Перемножив матрицы А -1 и В -1 , получим матрицу обратного преобразования:

Запишем обратное преобразование также и в виде формул

Перспективная проекция

Перспективную проекцию (рис. 2.17) сначала рассмотрим при вертикальном расположении камеры, когда а=β = 0. Такую проекцию можно себе пред­ставить как изображение на стекле, через которое смотрит наблюдатель, рас­положенный сверху в точке (х, у, z ) = (0, 0, z k). Здесь плоскость проецирова­ния параллельна плоскости (хОу).

Исходя из подобия треугольников, запишем такие пропорции:

Учитывая также координату Z:

В матричной форме преобразования координат можно записать так:

Рис. 2.17. Перспективная проекция

Обратите внимание на то, что здесь коэффициенты матрицы зависят от коор­динаты z (в знаменателе дробей). Это означает, что преобразование коор­динат является нелинейным (а точнее, дробно-линейным), оно относится к классу проективных преобразований.

Теперь рассмотрим общий случай - для произвольных углов наклона каме­ры (а и р) так же, как и для параллельной аксонометрической проекции. Пусть (х", у", z 1 ) - координаты для системы координат, повернутой относи­тельно начальной системы (х, у, z ) на углы α и β.

Запишем преобразования координат перспективной проекции в виде:

Последовательность преобразования координат можно описать так:

Преобразование в целом нелинейное. Его нельзя описать одной матрицей коэффициентов-констант для всех объектов сцены (хотя для преобразования координат можно использовать и матричную форму).

Для такой перспективной проекции плоскость проецирования перпендику­лярна лучу, исходящему из центра (х, у, z )= (0, 0, 0) и наклоненному под углом α, β. Если камеру отдалять от центра координат, то центральная проек­ция видоизменяется. Когда камера в бесконечности, центральная проекция вырождается в параллельную проекцию.

Укажем основные свойства перспективного преобразования. В центральной

проекции:

□ не сохраняется отношение длин и площадей;

□ прямые линии изображаются прямыми линиями;

□ параллельные прямые изображаются сходящимися в одной точке.

Последнее свойство широко используется в начертательной геометрии для ручного рисования на бумаге. Проиллюстрируем это на примере каркаса до­мика (рис. 2.18).

Существуют и другие перспективные проекции, которые различаются поло­жением плоскости проецирования и местом точки схождения лучей проеци­рования. Кроме того, проецирование может осуществляться не на плоскость, а, например, на сферическую или цилиндрическую поверхность.

Рассмотрим косоугольную проекцию, для которой лучи проецирования не перпендикулярны плоскости проецирования. Основная идея такой проекции - камера поднята на высоту h с сохранением вертикального положения плоскости проектирования (рис. 2.19).

Рис. 2.18. Параллельные линии изображаются в центральной проекции сходящимися в одной точке

Рис. 2.19. Косоугольная проекция

Получить такую проекцию можно следующим способом:

1. Выполняем поворот вокруг оси z на угол а.

2. Заменяем z " на -у", а.у" на z".

3. Выполняем сдвиг системы координат вверх на высоту камеры h

4. В плоскости (х", у", 0) строим перспективную проекцию уже рассмотрен­ным выше способом (точка схода лучей на оси z ).

Преобразование координат может быть описано таким образом. Сначала оп­ределяются (x", у", z ′).

А потом выполняется перспективное преобразование

Преимущество такой проекции заключается в сохранении параллельности вертикальных линий, что иногда полезно при изображении домов в архитек­турных компьютерных системах.

Примеры изображений в различных проекциях. Приведем примеры изо­бражений одинаковых объектов в различных проекциях. В качестве объектов будут кубы одинакового размера. Положение камеры определим углами на­клона α = 27°, β = 70°.

Пример аксонометрической проекции приведен на рис. 2.20.

Рис. 2.20. Аксонометрическая проекция

Теперь рассмотрим примеры для перспективной проекции. В отличие от параллельной проекции, изображение в перспективной проекции существенно зависит от положения плоскости проецирования и расстояния до камеры.

В оптических системах известно понятие фокусного расстояния. Чем больше фокусное расстояние объектива, тем меньше восприятие перспективы (рис. 2.21" и наоборот, для короткофокусных объективов перспектива наибольший (рис. 2.22). Данный эффект вы, наверное, уже замечали, если занимались съемками видеокамерой или фотоаппаратом. В наших примерах можно наблюдать некоторое соответствие величины расстояния от камеры до плоскости проецирования { z k – z пл ) и фокусного расстояния объектива. Это соответствие, однако, условно, аналогия с оптическими системами здесь неполная.

Для приведенных Ниже примеров (рис. 2.21, 2.22) z пл = 700. Углы наклона камеры α = 27°, β = 70°.

Рис. 2.21. Перспективная проекция для длиннофокусной камеры ( z K = 2000)

Рис. 2.22. Перспективная проекция для короткофокусной камеры ( z K = 1200)

В случае короткофокусной камеры (z K = 1200) восприятие перспективы наиболее заметно для кубов, которые расположены ближе всего к камере. Вертикальные линии объектов не являются вертикалями на проекции (объекты разваливаются").

Усмотрим примеры косоугольной проекции (рис. 2.23, 2.24). Для нее вер­тикальные линии объектов сохраняют вертикальное расположение на проекции. Положение камеры (точки схождения лучей проецирования) описывается углом поворота α = 27° и высотой подъема h = 500. Плоскость проециро­вания параллельна плоскости (х"Оу") и располагается на расстоянии z пл = 700.

Рис. 2.23. Косоугольная перспективная проекция для длиннофокусной камеры ( z K = 2000)

Рис. 2.24. Косоугольная перспективная проекция для короткофокусной камеры ( z K = 1200)

Рассмотрим еще один пример изображения в центральной проекции - тега в стиле фильма "Звездные войны":

Отображение в окне

Как мы уже рассмотрели выше, отображение на плоскость проецирования соответствует некоторому преобразованию координат. Это преобразование координат различно для разных типов проекции, но, так или иначе, осущест­вляется переход к новой системе координат - координатам проецирования. Координаты проецирования могут быть использованы для формирования изображения с помощью устройства графического вывода. Однако при этом могут понадобиться дополнительные преобразования, поскольку система ко­ординат в плоскости проецирования может не совпадать с системой коорди­нат устройства отображения. Например, должны отображаться объекты, из­меряемые в километрах, а в растровом дисплее единицей измерения является пиксел. Как выразить километры в пикселах?

Кроме того, вы, наверное, видели, что на экране компьютера можно показы­вать увеличенное, уменьшенное изображение объектов, а также их переме­щать. Как это делается?

Введем обозначения. Пусть (Хэ, Уэ, Z э) - это экранные координаты объектов в графическом устройстве отображения. Заметим, что не следует восприни­мать слово "экранные" так, будто речь идет только о дисплеях - все ниже­следующее можно отнести и к любым другим устройствам, использующим декартову систему координат. Координаты проецирования обозначим здесь как (X, Y, Z).

Назовем окном прямоугольную область вывода с экранными координатами

X э min Уэтп) - (Хэтах Уэтах)- Обычно Приходится Отображать В Окно ИЛИ ВСЮ

сцену, или отдельную ее часть (рис. 2.25).

Рис. 2.25. Отображение проекции сцены

а - границы сцены в координатах проекции; б - в окне часть сцены, в - вся сцена с сохранением пропорций вписана в окно

Преобразование координат проекции в экранные координаты можно задать как растяжение/сжатие и сдвиг:

Х Э = КХ + dx , ; Y Э = KY + dy ; Z э = KZ .

Такое преобразование сохраняет пропорции объектов благодаря одинаково­му коэффициенту растяжения/сжатия (К) для всех координат. Заметим, что для плоского отображения можно отбросить координату Z. Рассмотрим, как можно вычислить К, dx и dy . Например, необходимо впи­сать все изображение сцены в окно заданных размеров. Условие вписывания можно определить так:

Если прибавить (1) к (3), то получим:

Из неравенств (2) и (4) следует:

Решением системы (1)-(4) для K будет: К ≤ min {Кх, Ку} = К min .

Если значение К х или значение K Y равно бесконечности, то его необходим отбросить. Если оба - то значение К min можно задать равным единице. Дга| того чтобы изображение в окне имело наибольший размер, выберем К = К min Теперь можно найти dx . Из неравенства (1):

Из неравенства (3): I

Поскольку dx 1 < dx 2, то величину dx можно выбрать из интервала I dx 1 ≤dx ≤ dx 2. Выберем центральное расположение в окне: I

Аналогично найдем dy:

При таких значениях dx и dy центр сцены будет в центре окна.

В других случаях, когда в окне необходимо показывать с соответствующим масштабом лишь часть сцены, можно прямо задавать числовые значения масштаба (К) и координаты сдвига (dx , dy ). При проектировании интерфейса графической системы желательно ограничить выбор К, dx , dy диапазоном допустимых значений.

графических системах используются разнообразные способы задания масйаба отображения и определения границ сцены для показа в окне просмотра. Например, для сдвига часто используют ползунки скроллинга. Также "южно указывать курсором точку на сцене, и затем эта точка становится центральной точкой окна. Или можно очертить прямоугольник, выделяя грани­цы фрагмента сцены, - тогда этот фрагмент затем будет вписан в окно. Й так далее. Все эти способы отображения основываются на растяжении и сжатии (масштабировании), а также сдвиге, и описываются аффинным преобразованием координат.

Проецирование (лат. Projicio – бросаю вперёд) – процесс получения изображения предмета (пространственного объекта) на какой-либо поверхности с помощью световых или зрительных лучей (лучей, условно соединяющих глаз наблюдателя с какой-либо точкой пространственного объекта), которые называются проецирующими.

Известны два метода проецирования: центральное и параллельное .

Центральное проецирование заключается в проведении через каждую точку (А, В, С ,…) изображаемого объекта и определённым образом выбранный центр проецирования (S ) прямой линии (SA , SB , >… — проецирующего луча ).

Рисунок 1.1 – Центральное проецирование

Введём следующие обозначения (Рисунок 1.1):

S – центр проецирования (глаз наблюдателя);

π 1 – плоскость проекций;

A, B, C

SA , SB – проецирующие прямые (проецирующие лучи).

Примечание : левой клавишей мыши можно переместить точку в горизонтальной плоскости, при щелчке на точке левой клавишей мыши, изменится направление перемещения и можно будет ее переместить по вертикали.

Центральной проекцией точки называется точка пересечения проецирующей прямой, проходящей через центр проецирования и объект проецирования (точку), с плоскостью проекций.

Свойство 1 . Каждой точке пространства соответствует единственная проекция, но каждой точке плоскости проекций соответствует множество точек пространства, лежащих на проецирующей прямой.

Докажем это утверждение.

На рисунке 1.1: точка А 1 – центральная проекция точки А на плоскости проекций π 1 . Но эту же проекцию могут иметь все точки, лежащие на проецирующей прямой. Возьмём на проецирующей прямой SA точку С . Центральная проекция точки С (С 1) на плоскости проекций π 1 совпадает с проекцией точки А (А 1):

1. С ∈ SA ;
2. SC ∩ π 1 =C 1 → C 1 ≡ A 1 .

Следует вывод, что по проекции точки нельзя судить однозначно о её положении в пространстве.

Чтобы устранить эту неопределенность, т.е. сделать чертеж обратимым , введём еще одну плоскость проекций (π 2) и ещё один центр проецирования (S 2) (Рисунок 1.2).

Рисунок 1.2 – Иллюстрация 1-го и 2-го свойств

Построим проекции точки А на плоскости проекций π 2 . Из всех точек пространства только точка А имеет своими проекциями А 1 на плоскость π 1 и А 2 на π 2 одновременно. Все другие точки лежащие на проецирующих лучах будут иметь хотя бы одну отличную проекцию от проекций точки А (например, точка В ).

Свойство 2 . Проекция прямой есть прямая.

Докажем данное свойство.

Соединим точки А и В между собой (Рисунок 1.2). Получим отрезок АВ , задающий прямую. Треугольник ΔSAB задает плоскость, обозначенную через σ. Известно, что две плоскости пересекаются по прямой: σ∩π 1 =А 1 В 1 , где А 1 В 1 – центральная проекция прямой, заданной отрезком АВ .

Метод центрального проецирования – это модель восприятия изображения глазом, применяется главным образом при выполнении перспективных изображений строительных объектов, интерьеров, а также в кинотехнике и оптике. Метод центрального проецирования не решает основной задачи, стоящей перед инженером – точно отразить форму, размеры предмета, соотношение размеров различных элементов.

1.2. Параллельное проецирование

Рассмотрим метод параллельного проецирования. Наложим три ограничения, которые позволят нам, пусть и в ущерб наглядности изображения, получить чертёж более удобным для использования его на практике:

1. Удалим оба центра проекции в бесконечность. Таким образом, добьемся того, что проецирующие лучи из каждого центра станут параллельными, а, следовательно, соотношение истинной длины любого отрезка прямой и длины его проекции будут зависеть только от угла наклона этого отрезка к плоскостям проекций и не зависят от положения центра проекций;
2. Зафиксируем направление проецирования относительно плоскостей проекций;
3. Расположим плоскости проекций перпендикулярно друг другу, что позволит легко переходить от изображения на плоскостях проекций к реальному объекту в пространстве.

Таким образом, наложив эти ограничения на метод центрального проецирования, мы пришли к его частному случаю – методу параллельного проецирования (Рисунок 1.3).Проецирование, при котором проецирующие лучи, проходящие через каждую точку объекта, параллельно выбранному направлению проецирования P , называется параллельным.

Рисунок 1.3 – Метод параллельного проецирования

Введём обозначения:

Р – направление проецирования;

π 1 – горизонтальная плоскость проекций;

A, B – объекты проецирования – точки;

А 1 и В 1 – проекции точек А и В на плоскость проекций π 1 .

Параллельной проекцией точки называется точка пересечения проецирующей прямой, параллельной заданному направлению проецирования Р , с плоскостью проекций π 1 .

Проведём через точки А и В проецирующие лучи, параллельные заданному направлению проецирования Р . Проецирующий луч проведённый через точку А пересечёт плоскость проекций π 1 в точке А 1 . Аналогично проецирующий луч, проведённый через точку В пересечет плоскость проекций в точке В 1 . Соединив точки А 1 и В 1 , получим отрезок А 1 В 1 – проекция отрезка АВ на плоскость π 1 .

1.3. Ортогональное проецирование. Метод Монжа

Если направление проецирования Р перпендикулярно плоскости проекций p 1 , то проецирование называется прямоугольным (Рисунок 1.4),или ортогональным (греч. ortos – прямой, gonia – угол), если Р не перпендикулярно π 1 , то проецирование называется косоугольным .

Четырехугольник АА 1 В 1 В задаёт плоскость γ, которая называется проецирующей, поскольку она перпендикулярна к плоскости π 1 (γ⊥π 1). В дальнейшем будем использовать только прямоугольное проецирование.

Рисунок 1.4 – Ортогональное проецирование Рисунок 1.5- Монж, Гаспар (1746-1818)

Основоположником ортогонального проецирования считается французский учёный Гаспар Монж (Рисунок 1.5).

До Монжа строители, художники и учёные обладали довольно значительными сведениями о проекционных способах, и, всё же, только Гаспар Монж является творцом начертательной геометрии как науки.

Гаспар Монж родился 9 мая 1746 года в небольшом городке Боне (Бургундия) на востоке Франции в семье местного торговца. Он был старшим из пяти детей, которым отец, несмотря на низкое происхождение и относительную бедность семьи, постарался обеспечить самое лучшее образование из доступного в то время для выходцев из незнатного сословия. Его второй сын, Луи, стал профессором математики и астрономии, младший — Жан также профессором математики, гидрографии и навигации. Гаспар Монж получил первоначальное образование в городской школе ордена ораторианцев. Окончив её в 1762 году лучшим учеником, он поступил в колледж г. Лиона, также принадлежавший ораторианцам. Вскоре Гаспару доверяют там преподавание физики. Летом 1764 года Монж составил замечательный по точности план родного города Бона. Необходимые при этом способы и приборы для измерения углов и вычерчивания линий были изобретены самим составителем.

Во время обучения в Лионе получил предложение вступить в орден и остаться преподавателем колледжа, однако, вместо этого, проявив большие способности к математике, черчению и рисованию, сумел поступить в Мезьерскую школу военных инженеров, но (из-за происхождения) только на вспомогательное унтер-офицерское отделение и без денежного содержания. Тем не менее, успехи в точных науках и оригинальное решение одной из важных задач фортификации (о размещении укреплений в зависимости от расположения артиллерии противника) позволили ему в 1769 году стать ассистентом (помощником преподавателя) математики, а затем и физики, причём уже с приличным жалованием в 1800 ливров в год.

В 1770 году в возрасте 24-х лет Монж занимает должность профессора одновременно по двум кафедрам — математики и физики, и, кроме того, ведёт занятия по резанию камней. Начав с задачи точной резки камней по заданным эскизам применительно к архитектуре и фортификации, Монж пришёл к созданию методов, обобщённых им впоследствии в новой науке – начертательной геометрии, творцом которой он по праву считается. Учитывая возможность применения методов начертательной геометрии в военных целях при строительстве укреплений, руководство Мезьерской школы не допускало открытой публикации вплоть до 1799 года, книга вышла под названием Начертательная геометрия (Géométrie descriptive ) (стенографическая запись этих лекций была сделана в 1795 году). Изложенный в ней подход к чтению лекций по этой науке и выполнению упражнений сохранился до наших дней. Еще один значительный труд Монжа – Приложение анализа к геометрии (L’application de l’analyse à la géometrie , 1795) – представляет собой учебник аналитической геометрии, в котором особый акцент делается на дифференциальных соотношениях.

В 1780 был избран членом Парижской академии наук, в 1794 стал директором Политехнической школы. В течение восьми месяцев занимал пост морского министра в правительстве Наполеона, заведовал пороховыми и пушечными заводами республики, сопровождал Наполеона в его экспедиции в Египет (1798–1801). Наполеон пожаловал ему титул графа, удостоил многих других отличий.

Метод изображения объектов по Монжу заключается в двух основных моментах:

1. Положение геометрического объекта в пространстве, в данном примере точки А , рассматривается относительно двух взаимно перпендикулярных плоскостей π 1 и π 2 (Рисунок 1.6).

Они условно разделяют пространство на четыре квадранта. Точка А расположена в первом квадранте. Декартова система координат послужила основой для проекций Монжа. Монж заменил понятие осей проекций на линию пересечения плоскостей проекций (координатные оси) и предложил совместить координатные плоскости в одну путем поворота их вокруг координатных осей.

Рисунок 1.6 – Модель построения проекций точки

π 1 – горизонтальная (первая) плоскость проекций

π 2 – фронтальная (вторая) плоскость проекций

π 1 ∩π 2 — ось проекций (обозначим π 2 /π 1)

Рассмотрим пример проецирования точки А на две взаимно перпендикулярные плоскости проекций π 1 и π 2 .

Опустим из точки А перпендикуляры (проецирующие лучи) на плоскости π 1 и π 2 и отметим их основания, то есть точки пересечения этих перпендикуляров (проецирующих лучей) с плоскостями проекций. А 1 – горизонтальная (первая) проекция точки А; А 2 – фронтальная (вторая) проекция точки А; АА 1 и АА 2 – проецирующие прямые. Стрелки показывают направление проецирования на плоскости проекций π 1 и π 2 . Такая система позволяет однозначно определить положение точки относительно плоскостей проекций π 1 и π 2:

АА 1 ⊥π 1

А 2 А 0 ⊥π 2 /π 1 АА 1 = А 2 А 0 — расстояние от точки А до плоскости π 1

АА 2 ⊥π 2

А 1 А 0 ⊥π 2 /π 1 АА 2 = А 1 А 0 — расстояние от точки А до плоскости π 2

2. Совместим поворотом вокруг оси проекций π 2 /π 1 плоскости проекций в одну плоскость (π 1 с π 2), но так, чтобы изображения не накладывались друг на друга, (в направлении α, Рисунок 1.6), получим изображение, называемое прямоугольным чертежом (Рисунок 1.7):

Рисунок 1.7 – Ортогональный чертеж

Прямоугольный или ортогональный носит название эпюр Монжа .

Прямая А 2 А 1 называется линией проекционной связи , которая соединяет разноимённые проекции точки (А 2 — фронтальную и А 1 — горизонтальную) всегда перпендикулярна оси проекций (оси координат) А 2 А 1 ⊥π 2 /π 1 . На эпюре отрезки, обозначенные фигурными скобками, представляют собой:

• А 0 А 1 – расстояние от точки А до плоскости π 2 , соответствующее координате y А;
• А 0 А 2 – расстояние от точки А до плоскости π 1 , соответствующее координате z А.

1.4. Прямоугольные проекции точки. Свойства ортогонального чертежа

1. Две прямоугольные проекции точки лежат на одной линии проекционной связи, перпендикулярной к оси проекций.

2. Две прямоугольные проекции точки однозначно определяют её положение в пространстве относительно плоскостей проекций.

Убедимся в справедливости последнего утверждения, для чего повернём плоскость π 1 в исходное положение (когда π 1 ⊥π 2). Для того, чтобы построить точку А необходимо из точек А 1 и А 2 восстановить проецирующие лучи, а фактически – перпендикуляры к плоскостям π 1 и π 2 , соответственно. Точка пересечения этих перпендикуляров фиксирует в пространстве искомую точку А . Рассмотрим ортогональный чертеж точки А (Рисунок 1.8).

Рисунок 1.8 – Построение эпюра точки

Введём третью (профильную) плоскость проекций π 3 перпендикулярную π 1 и π 2 (задана осью проекций π 2 /π 3).

Расстояние от профильной проекции точки до вертикальной оси проекций А ‘ 0 A 3 позволяет определить расстояние от точки А до фронтальной плоскости проекций π 2 . Известно, что положение точки в пространстве можно зафиксировать относительно декартовой системы координат с помощью трёх чисел (координат) A (X A ; Y A ; Z A) или относительно плоскостей проекций с помощью её двух ортогональных проекций (A 1 =(X A ; Y A); A 2 =(X A ; Z A)). На ортогональном чертеже по двум проекциям точки можно определить три её координаты и, наоборот, по трём координатам точки, построить её проекции (Рисунок 1.9, а и б).

Рисунок 1.9 – Построение эпюра точки по её координатам

По расположению на эпюре проекций точки можно судить о её расположении в пространстве:

• А — А 1 лежит под осью координат X , а фронтальная — А 2 – над осью X , то можно говорить, что точка А принадлежит 1-му квадранту;
• если на эпюре горизонтальная проекция точки А — А 1 лежит над осью координат X , а фронтальная — А 2 – под осью X , то точка А принадлежит 3-му квадранту;
• А — А 1 и А 2 лежат над осью X , то точка А принадлежит 2-му квадранту;
• если на эпюре горизонтальная и фронтальная проекции точки А — А 1 и А 2 лежат под осью X , то точка А принадлежит 4-му квадранту;
• если на эпюре проекция точки совпадает с самой точкой, то значит – точка принадлежит плоскости проекций;
• точка, принадлежащая плоскости проекций или оси проекций (оси координат), называется точкой частного положения .

Для определения в каком квадранте пространства расположена точка, достаточно определить знак координат точки.

Зависимости квадранта положения точки и знаков координат

	X	Y	Z
I	+	+	+
II	+	—	+
III	+	—	—
IV	+	+	—

Упражнение

Построить ортогональные проекции точки с координатами А (60, 20, 40) и определить в каком квадранте расположена точка.

Решение задачи: по оси OX отложить значение координаты X A =60 , затем через эту точку на оси OX восстановить линию проекционной связи, перпендикулярную к OX , по которой вверх отложить значение координаты Z A =40 , а вниз – значение координаты Y A =20 (Рисунок 1.10). Все координаты положительные, значит точка расположена в I квадранте.

Рисунок 1.10 – Решение задачи

1.5. Задачи для самостоятельного решения

1. По эпюру определите положение точки относительно плоскостей проекций (Рисунок 1.11).

Рисунок 1.11

2. Достройте недостающие ортогональные проекции точек А , В , С на плоскости проекций π 1 , π 2 , π 3 (Рисунок 1.12).

Рисунок 1.12

3. Постройте проекции точки:

• Е , симметричной точке А относительно плоскости проекций π 1 ;
• F , симметричной точке В относительно плоскости проекций π 2 ;
• G , симметричной точке С относительно оси проекций π 2 /π 1 ;
• H , симметричной точке D относительно биссекторной плоскости второго и четвертого квадрантов.

4. Постройте ортогональные проекции точки К , расположенной во втором квадранте и удаленной от плоскостей проекций π 1 на 40 мм, от π 2 — на 15 мм.

На какой-либо поверхности (плоской, цилиндрической, сфериче­ской, конической) с помощью проецирующих лучей.

Проецирование может осуществляться различными методами.

Методом проецирования называется способ получения изо­бражений с помощью определенной, присущей только ему сово­купности средств проецирования (центра проецирования, на­правления проецирования, проецирующих лучей, плоскостей (по­верхностей) проекций), которые определяют результат - соот­ветствующие проекционные изображения и их свойства.

Для того чтобы получить любое изображение предмета на плоскости, необходимо расположить его перед плоскостью про­екций и из центра проецирования провести воображаемые про­ецирующие лучи, пронизывающие каждую точку поверхности предмета. Пересечение этих лучей с плоскостью проекций дает множество точек, совокупность которых создает изображение предмета, называемое его проекцией. Это общее определение рассмотрим на примере проецирования точки, прямой, треуголь­ника и треугольной призмы на плоскость проекций H.

Проецирование точки (рис. 52, а). Возьмем в пространстве произвольную точку А и расположим ее над плоскостью проек­ций H. Проведем через точку А проецирующий луч так, чтобы он пересек плоскость H в некоторой точке а, которая будет являться проекцией точки А. (Здесь и в дальнейшем будем обозначать точки, взятые на предмете, прописными буквами чертежного шрифта, а их проекции - строчными.) Как видим, методом проецирования можно получить проекцию нульмерного объекта- точки.

Проецирование прямой (рис. 52, б). Представим себе прямую как совокупность точек. Используя метод проецирования, прове­дем множество параллельных проецирующих лучей через точки, из которых состоит прямая, до пересечения их с плоскостью про­екций. Полученные проекции точек составят проекцию заданной прямой - одномерного объекта.

Проецирование треугольника (рис. 52, в). Расположим тре­угольник ABC перед плоскостью H. Приняв вершины треуголь­ника за отдельные точки А, В, С, спроецируем каждую из них на плоскость проекций. Получим проекции вершин треугольника - a, b, с. Последовательно соединив проекции вершин (а и b; b и с; с и а), получим проекции сторон треугольника (ab, bc, ca). Часть плоскости, ограниченная изображением сторон треугольника abc, будет являться проекцией треугольника ABC на плоскости H Следовательно, методом проецирования можно получить проек­цию плоской фигуры - двухмерного объекта.

Проецирование призмы (рис. 52, г). Для примера возьмем наклонную треугольную призму и спроецируем ее на плоскость проекций H. В результате проецирования призмы на плоскость H получают изображения (проекции) ее оснований - треуголь­ников - abc и a 1 b 1 c 1 и боковых граней - прямоугольников abb 1 a 1 и bcc 1 b 1 . Так в результате проецирования на плоскости H получают проекцию треугольной призмы. Следовательно, с помощью метода проецирования можно отобразить любой трех­мерный объект.

Рис. 52. Проецирование нуль-, одно-, двух- и трехмерных объектов: а - точка;
б - прямая; в - треугольник; г - призма

Таким образом, методом проецирования можно отобразить на плоскости любой объект (нуль-, одно-, двух- и трехмерный). В этом отношении метод проецирования является универсальным.

Сущность проецирования легче понять, если вспомнить получение изображения в кинотеатре: световой поток лампы кинопроектора проходит через пленку и отбрасывает изображение на полотно. При этом изображение на киноэкране будет в несколько раз больше изображения на кинопленке.

Существует центральное (или перспективное) и параллельное проецирование. Параллельное проецирование бывает прямо­угольным (ортогональным) или косоугольным (табл. 5).

5. Методы проецирования

Центральное проецирование (перспектива) характеризуется тем, что проецирующие лучи исходят из одной точки (S), назы­ваемой центром проецирования . Полученное изображение назы­вается центральной проекцией .

Перспектива передает внешнюю форму предмета так, как воспринимает его наше зрение.

При центральном проецировании, если предмет находит­ся между центром проецирования и плоскостью проекций, размеры проекции будут больше оригинала; если предмет расположен за плоскостью проекций, то размеры проекции станут меньше действи­тельных размеров изображаемого предмета.

Параллельное проецирование характеризуется тем, что про­ецирующие лучи параллельны между собой. В этом случае предполагается, что центр проецирования (S) удален в бесконеч­ность.

Изображения, полученные в результате параллельного про­ецирования, называются параллельными проекциями.

Если проецирующие лучи параллельны между собой и пада­ют на плоскость проекций под прямым углом, то проецирование называется прямоугольным (ортогональным), а полученные проекции - прямоугольными (ортогональными). Если проеци­рующие лучи параллельны между собой, но падают на плоскость Проекций под углом, отличным от прямого, то проецирование на­зывается косоугольным, а полученная проекция - косоугольной. При проецировании объект располагают перед плоскостью про­екций таким образом, чтобы на ней получилось изображение, несущее наибольшую информацию о форме.

Проекция изображения происходит всякий раз, когда плоское изображение отображается на изогнутой поверхности или наоборот, и в частности, проекции повсеместно используются в панорамной фотографии. Проекция осуществляется, когда картограф отображает сферический глобус Земли на плоском листе бумаги, например. Поскольку полное поле зрения вокруг нас может рассматриваться как поверхность сферы (для всех углов зрения), для фотографий, которые будут показаны на плоском мониторе или отпечатаны, требуется аналогичная проекция сферы в плоскость.

Для малых углов зрения отобразить изображение на плоском листе бумаги относительно легко, поскольку обозреваемый сектор практически плоский. При отображении сферического изображения на плоской поверхности некоторые искажения неустранимы, поэтому каждый тип проекции пытается минимизировать один тип искажения за счёт остальных. По мере расширения угла зрения рассматриваемые сектора становятся всё более изогнутыми, и следовательно, разница между типами панорамных проекций становится более выраженной. Момент использования каждой из проекций зависит преимущественно от изображаемого предмета и применения; здесь мы сфокусируемся на нескольких типах проекций, которые наиболее распространены в цифровой фотографии. Многие типы проекций, обсуждаемые в данной главе, могут использоваться в качестве выходного формата в нескольких пакетах программ сборки панорам; PTAssembler позволяет использовать все перечисленные проекции.

Типы проекции изображений в фотографии

Если все эти типы проекции изображений выглядят несколько обескураживающе, попробуйте сперва прочитать и осознать различие между прямоугольной и цилиндрической проекциями (выделены), поскольку они наиболее широко используются при сборке цифровых панорам.

Эквидистантная проекция отображает координаты широты и долготы сферического глобуса непосредственно на горизонтальные и вертикальные координаты сетки, где сетка имеет ширину примерно вдвое больше высоты. Горизонтальное растяжение, как следствие, усиливается по направлению к полюсам, так что северный и южный полюсы оказываются растянуты на всю верхнюю и нижнюю границы плоской сетки, соответственно. Эквидистантные проекции могут показать полный вертикальный и горизонтальный углы вплоть до 360 градусов.

Цилиндрическая проекция изображения аналогична эквидистантной, за исключением того, что по мере приближения к северному и южному полюсам объекты также растягиваются по вертикали так что на полюсах достигается бесконечное растяжение по вертикали (так что горизонтальная линия наверху и внизу плоской сетки отсутствует). Именно по этой причине цилиндрические проекции непригодны для изображений с большим вертикальным углом зрения. Цилиндрические проекции также являются стандартным типом, отображаемым традиционными панорамными плёночными камерами с поворотным объективом. Цилиндрические проекции сохраняют более точные относительные размеры объектов, чем прямоугольные, однако достигается это за счёт искривления линий, параллельных линии зрения (которые иначе оставались бы прямыми).

Прямоугольная проекция изображения имеет основное преимущество в том, что отображает прямые линии в трёхмерном пространстве в прямые линии на плоской двумерной сетке. Этот тип проекции соответствует тому, который создаёт большинство обычных широкоугольных объективов, так что она, вероятно, является наиболее понятной. Её основной недостаток состоит в том, что она может существенно преувеличить перспективу по мере увеличения угла обзора, что приводит к видимому завалу объектов к границам кадра. Именно по этой причине прямоугольные проекции обычно не рекомендуются для углов зрения, которые существенно превышают 120 градусов.

Рыбий глаз - это проекция изображения, целью которой является создание плоской сетки, где расстояние от центра сетки примерно пропорционально действительному углу зрения; она образует изображение, которое выглядит похоже на отражение от металлической сферы. Как правило такая проекция не используется в качестве выходного формата панорамной фотографии, но вместо того она может представлять исходные изображения, если для съёмки таковых использовался объектив типа «рыбий глаз». Эта проекция к тому же ограничена вертикальным и горизонтальным углом обзора 180 градусов или менее, порождая изображение, которое помещается в круг. Её характеризует нарастающее искривление линий (которые иначе были бы прямыми) по мере удаления от центра изображения. Камера с объективом типа «рыбий глаз» исключительно полезна при создании панорам, которые покрывают всю сферу зрения, поскольку достаточно будет собрать небольшое число снимков.

Проекция Меркатора наиболее близко соотносится с цилиндрической и эквидистантной проекциями; она является компромиссом между этими двумя типами, обеспечивая меньшее растяжение по вертикали и более широкий употребимый угол зрения, чем цилиндрическая проекция, но с более сильным искривлением линий. Эта проекция, вероятно, является наиболее узнаваемой, поскольку используется в плоских картах мира. Отметим также, что альтернативная форма этой проекции (поперечный Меркатор) может использоваться для вертикальных панорам большой высоты.

Синусоидальная проекция изображения пытается сохранить равные площади во всех участках сетки. Если развернуть глобус в плоскость, можно вообразить, что такую проекцию можно свернуть обратно, чтобы сформировать сферу, которая будет идентична исходной по форме и площади поверхности. Характеристика равной площади полезна, поскольку если записывать плоскую проекцию сферического изображения, она сохранит неизменное горизонтальное и вертикальное разрешение по всему изображению. Эта проекция подобна рыбьему глазу и стереографической, за вычетом того, что сохраняет абсолютно горизонтальные линии из исходной сферы.

Стереографическая проекция очень похожа на рыбий глаз, но при этом сохраняет лучшее ощущение перспективы, увеличивая растяжение объектов по мере их удаления от точки перспективы. Подобная выделяющая перспективу характеристика в чём-то похожа на прямоугольную проекцию, хотя здесь она менее выражена.

Примеры: широкое горизонтальное поле зрения

Как все эти проекции изображения в действительности влияют на панорамную фотографию? Следующая серия снимков используется для наглядной демонстрации различий между двумя типами проекции, которые наиболее часто встречаются в программах сборки панорам: прямоугольной и цилиндрической. Снимки подобраны так, чтобы показать только различия в искажениях для широкого горизонтального угла зрения; вертикальные панорамы подобраны далее для иллюстрации разницы в вертикальных искажениях между другими типами проекций.

Первый пример демонстрирует, как прямоугольная проекция могла бы отобразить фотопанораму из трёх снимков, показанных выше.

Обратите внимание на значительные искажения по краям угла зрения, вдобавок к драматической потере разрешения вследствие растягивания изображения. Следующий снимок демонстрирует, как выглядело бы сильно искажённое изображение, показанное выше, если бы его обрезали по горизонтальному углу зрения, составляющему всего 120 градусов.

Как можно видеть, такая кадрированная прямоугольная проекция производит вполне приятное впечатление, поскольку все прямые архитектурные линии в сборке остаются прямыми. С другой стороны, это достигается за счёт относительного размера объектов в пределах угла зрения; объекты на границах угла зрения (левый и правый края) значительно увеличены по сравнению с объектами в центре (башня со входом внизу).

Следующий пример демонстрирует, как выглядел бы результат сборки с использованием цилиндрической проекции. Её преимущество заключается в относительно равномерном распределении разрешения, а кроме того, она требует минимального кадрирования. Вдобавок, разница между цилиндрической и эквидистантной проекциями пренебрежимо мала для фотографий, которые не имеют исключительно большого вертикального угла зрения (как в следующем примере).

Примеры: высокое вертикальное поле зрения

Следующие примеры иллюстрируют разницу между типами проекций для вертикальной панорамы (с большим вертикальным полем зрения). Она даёт шанс показать разницу между эквидистантной, цилиндрической и проекцией Меркатора, которые в предыдущем примере выглядели бы практически одинаково (для широкого горизонтального угла зрения).

Примечание: точка перспективы для этой панорамы установлена в основании башни, и как следствие, действительный вертикальный угол зрения выглядит так, как если бы поле зрения составляло 140 градусов (как если бы точка перспективы была на половинной высоте).

	Поперечный Меркатор

Такой большой вертикальный угол зрения позволяет нам чётко увидеть, как каждая из выбранных проекций изображения отличается по степени вертикального растяжения/сжатия. Эквидистантная проекция сжимает вертикальную перспективу настолько сильно, что теряет ощущение огромной высоты, которое посещает непосредственного наблюдателя. По этой причине эквидистантная проекция рекомендуется, только когда это абсолютно необходимо (как например, для панорам с широчайшим полем зрения как по вертикали, так и по горизонтали).

Все три показанных проекции призваны сохранить практически прямые вертикальные линии; поперечная проекция Меркатора справа вносит некоторое скругление с целью сохранить более реалистичную (субъективно) перспективу. Этот тип проекции часто используется для экстремально больших вертикальных углов зрения. Заметим также, насколько хорошо эта проекция сохраняет исходный вид каждого из исходных снимков.

Разница между прямоугольной и цилиндрической проекциями для такого узкого горизонтального угла зрения едва заметна, так что прямоугольная проекция пропущена.

Калькуляторы панорамного поля зрения

Следующий калькулятор можно использовать для оценки горизонтального и вертикального углов зрения вашей камеры при использовании объективов с различными фокусными расстояниями, что может помочь в оценке подходящего типа проекции.

Проецирование - это процесс получения проекций предмета на какой-либо поверхности (плоской, цилиндрической, сферической, конической) с помощью проецирующих лучей.

Методом проецирования
называется способ получения изображений с помощью определенной, присущей только ему совокупности средств проецирования (центра проецирования, направления проецирования, проецирующих лучей, плоскостей (поверхностей) проекций), которые определяют результат - соответствующие проекционные изображения и их свойства.
Для того чтобы получить любое изображение предмета на плоскости, необходимо расположить его перед плоскостью проекций и из центра проецирования провести воображаемые проецирующие лучи, пронизывающие каждую точку поверхности предмета. Пересечение этих лучей с плоскостью проекций дает множество точек, совокупность которых создает изображение предмета, называемое его проекцией. Это общее определение рассмотрим на примере проецирования точки, прямой, треугольника и треугольной призмы на плоскость проекций H.

Проецирование точки (рис. а).
Возьмем в пространстве произвольную точку А и расположим ее над плоскостью проек­ций H. Проведем через точку А проецирующий луч так, чтобы он пересек плоскость H в некоторой точке а, которая будет являться проекцией точки А. (Здесь и в дальнейшем будем обозначать точки, взятые на предмете, прописными буквами чертежного шрифта, а их проекции - строчными.) Как видим, методом проецирования можно получить проекцию нульмерного объекта- точки.

Проецирование прямой (рис. б).
Представим себе прямую как совокупность точек. Используя метод проецирования, проведем множество параллельных проецирующих лучей через точки, из которых состоит прямая, до пересечения их с плоскостью проекций. Полученные проекции точек составят проекцию заданной прямой - одномерного объекта.


Проецирование треугольника (рис. в).
Расположим треугольник ABC перед плоскостью H. Приняв вершины треуголь­ника за отдельные точки А, В, С, спроецируем каждую из них на плоскость проекций. Получим проекции вершин треугольника - a, b, с. Последовательно соединив проекции вершин (а и b; b и с; с и а), получим проекции сторон треугольника (ab, bc, ca). Часть плоскости, ограниченная изображением сторон треугольника abc, будет являться проекцией треугольника ABC на плоскости H Следовательно, методом проецирования можно получить проекцию плоской фигуры - двухмерного объекта.

3.


Проецирование призмы (рис. г).
Для примера возьмем наклонную треугольную призму и спроецируем ее на плоскость проекций H. В результате проецирования призмы на плоскость H получают изображения (проекции) ее оснований - треугольников - abc и a1b1c1 и боковых граней - прямоугольников abb1a1 и bcc1b1. Так в результате проецирования на плоскости H получают проекцию треугольной призмы. Следовательно, с помощью метода проецирования можно отобразить любой трехмерный объект

4.

Таким образом, методом проецирования можно отобразить на плоскости любой объект (нуль-, одно-, двух- и трехмерный). В этом отношении метод проецирования является универсальным.Сущность проецирования легче понять, если вспомнить получение изображения в кинотеатре: световой поток лампы кинопроектора проходит через пленку и отбрасывает изображение на полотно. При этом изображение на киноэкране будет в несколько раз больше изображения на кинопленке.
Центральное проецирование (перспектива) характеризуется тем, что проецирующие лучи исходят из одной точки (S), называемой центром проецирования. Полученное изображение называется центральной проекцией.

Перспектива передает внешнюю форму предмета так, как воспринимает его наше зрение.

При центральном проецировании, если предмет находится между центром проецирования и плоскостью проекций, размеры проекции будут больше оригинала; если предмет расположен за плоскостью проекций, то размеры проекции станут меньше действительных размеров изображаемого предмета.

Параллельное проецирование характеризуется тем, что проецирующие лучи параллельны между собой. В этом случае предполагается, что центр проецирования (S) удален в бесконечность.
Изображения, полученные в результате параллельного проецирования, называются параллельными проекциями.

Если проецирующие лучи параллельны между собой и падают на плоскость проекций под прямым углом, то проецирование называется прямоугольным (ортогональным), а полученные проекции - прямоугольными (ортогональными).
Если проецирующие лучи параллельны между собой, но падают на плоскость Проекций под углом, отличным от прямого, то проецирование называется косоугольным, а полученная проекция - косоугольной. При проецировании объект располагают перед плоскостью проекций таким образом, чтобы на ней получилось изображение, несущее наибольшую информацию о форме.
Существует центральное (или перспективное) и параллельное проецирование. Параллельное проецирование бывает прямоугольным (ортогональным) или косоугольным

5.

---